SMURF Workshop: Survey Methods and their use in Related Fields, August 2018, Institute of Statistics, University of Neuchâtel
SMURF Workshop: Survey Methods and their use in Related Fields
20 - 22 August 2018, Neuchâtel, Switzerland
We aim at gathering researchers working in the field together with researchers who have used the theory of sampling in finite population in a different field of Science.
The goal of such an event is to review the state-of-the-art methods as well as to shed the light on some future perspectives of survey sampling, one of the most ancient field of statistics.
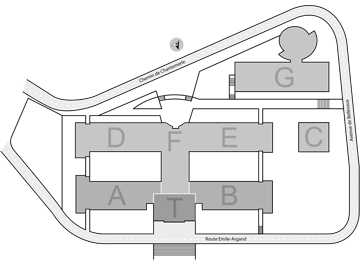
Venue : University of Neuchâtel
Faculty of Science
Auditoire Abraham-Louis Guillaume (ALG F200),
wing F (opposite to the lake), 2nd floor
Rue Emile Argand 11
2000 Neuchâtel
Confirmed Speakers:
- Simon Barthelmé (CNRS and Université Grenoble-Alpes)
- Yves Berger (University of Southampton)
- Patrice Bertail (Université Paris X - Nanterre)
- F. Jay Breidt (Colorado State University)
- Yann Busnel (IMT-Atlantique, Rennes)
- Guillaume Chauvet (ENSAI, Rennes)
- Lorenzo Fattorini (Università degli Studi di Siena)
- Mathieu Gerber (University of Bristol)
- David Haziza (University of Montréal)
- Vincent Loonis (INSEE, Paris)
- Hendrik P. Lopuhaä (Delft University of Technology)
- Jean Opsomer (Colorado State University & Westat)
- Takumi Saegusa (University of Maryland)
- Yves Tillé (Université de Neuchâtel)
Price : 250 CHF (includes coffee breaks, lunches and social dinner on Tuesday)
Date : 20-22 August 2018
Organizers:
- Guillaume Chauvet (ENSAI)
- Yves Tillé (Université de Neuchâtel)
- Matthieu Wilhelm (Université de Neuchâtel)
Supported by the French Statistical Society (SFdS).

SMURF Workshop: Survey Methods and their use in Related Fields
20 - 22 August 2018, Neuchâtel, Switzerland
Workshop schedule
The lectures will take place in the room F 200 " Auditoire Louis-Guillaume", second floor in the UniMail Building, Rue Emile-Argand 11, 2000, Neuchâtel.
Monday, 20 August 2018
08:30 - 09:10 Registration
09:15 - 09:30 Opening, Matthieu Wilhelm, Université de Neuchâtel
09:30 - 10:20 Revisiting design-based inference, Jean Opsomer, Colorado State University & Westat
10:20 - 10:50 Coffee Break
10:50 - 11:20 Data sub-sampling with determinantal point processes, Simon Barthelmé, CNRS – Université Grenoble-Alpes
11:20 - 12:10 Determinantal sampling design, Vincent Loonis, INSEE, Paris
12:10 - 14:00 Lunch break
14:00 - 14:50 A challenge for statisticians: the design-based spatial interpolation, Lorenzo Fattorini, Università degli Studi di Siena
14:50 - 15:40 Properties of pivotal sampling : applications to spatial sampling and to sampling in dataflows, Guillaume Chauvet, ENSAI, Rennes
15:40 - 16:10 Break
___________________________________________________________________________
Tuesday, 21 August 2018
09:00 - 09:50 Fast procedures for selecting unequal probability samples from a stream, Yves Tillé, Université de Neuchâtel
09:50 - 10:40 How to generate uniform Samples on large-scale data streams, Yann Busnel, IMT-Atlantique, Rennes
10:40 - 11:10 Coffee Break
11:10 - 12:00 Estimation in the presence of influential units in finite population sampling: an overview, David Haziza, Université de Montréal
12:00- 12:50 An empirical likelihood approach for modelling survey data, Yves Berger, University of Southampton
12:50 - 14:00 Lunch Break
14:00 - 18:00 Social Event
19:30 - 21:00 Social Dinner
___________________________________________________________________________
Wednesday, 22 August 2018
09:15 - 10:05 Survey methods and their use in Monte Carlo algorithms, Mathieu Gerber, University of Bristol
10:05 - 10:35 Coffee Break
10:35 - 11:25 Functional central limit theorems for single-stage sampling designs, Rik Lopuhäa, TU Delft
11:25 - 12:15 Large sample theory for merged data from multiple sources, Takumi Saegusa, University of Maryland
12:15 - 14:00 Lunch Break
14:00 - 14:50 Exponential bounds for sampling designs, Patrice Bertail, Université Paris X - Nanterre
14:50 - 15:40 On testing for informative selection in survey sampling, F. Jay Breidt, Colorado State University
15:40 - 16:00 Concluding remarks, Yves Tillé, Université de Neuchâtel
Abstracts
Data sub-sampling with determinantal point processes
Simon Barthelmé, CNRS – Université Grenoble-Alpes
Determinantal Point Processes (DPPs) are a class of point processes that exhibit "repulsion". This property can be leveraged to obtain high-diversity subsets, meaning that DPPs can be used to sub-sample various objects (surfaces, datasets, graphs, etc.) with relatively high fidelity.
This idea has been suggested by several authors and holds tremendous theoretical appeal. However, many difficulties crop up in the implementation, and our goal has been to lift some of them.
One aspect is that DPPs come in two variants: fixed sample size (so-called k-DPPs) and varying sample size. DPPs with varying sample sizes are more tractable, since their inclusion probabilities admit a closed form. k-DPPs make more sense in many applications, but are less tractable, since inclusion probabilities are much harder to compute. We show that k-DPPs and DPPs are asymptotically equivalent, which leads to tractable formulas for inclusion probabilities.
Joint work with Pierre Olivier Amblard and Nicolas Tremblay.
An empirical likelihood approach for modelling survey data
Yves Berger, University of Southampton
Data are often selected with unequal probabilities from a clustered and stratified population. We propose a design-based empirical likelihood approach for regression parameters of generalised linear models. It differs from the mainstream (pseudo-)empirical likelihood approach, because it takes into account of the selection process. It provides asymptotically valid inference for the finite population parameters; that is, it gives consistent maximum empirical likelihood estimators and pivotal empirical likelihood ratio statistics. Hence, this approach can be used for point estimation, hypothesis testing and confidence intervals, without the need of variance estimates or linearisation. We will show how the approach can be extended for hierarchical models. We will also show how nonresponse can be taken into account. We will show that standard estimators such as Horvitz-Thompson, regression and calibration estimators are particular cases of the general approach proposed. We will use the 2006 PISA survey data as an illustrative example.
Survey sampling for big data
Patrice Bertail, Université Paris X - Nanterre
Subsampling methods as well as general sampling methods appear as a natural tools to handle very large database (big data in the individual dimension) when traditional statistical methods or statistical learning algorithms fail to be implemented on too large datasets. The choice of the weights of the survey sampling scheme may reduce the loss implied by the choice of a much more smaller sampling size (according to the problem of interest).
I will first recall some asymptotic results for general survey sampling based empirical processes, indexed by class of functions (see Bertail and Clémençon, 2016, Scandinavian Journal of Statistics), for Poisson type and conditional Poisson (rejective) survey samplings. These results may be extended to a large class of survey sampling plans via the notion of negative association of most survey sampling plans (Bertail, Rebecq, 2017).
However when one is interested in controlling generalization capability of statistical learning algorithms based on survey sampling techniques, asymptotic results are not sufficient. Hoeffding or Bennett type inequalities, classical deviation inequalities in the i.i.d. setting can be applied directly to Poisson or associated survey sampling plan leading however to suboptimal bounds . We show here how to overcome this difficulty for rejective sampling or conditional sampling plans. In particular, the Bennet/Bernstein type bounds established highlight the effect of the asymptotic variance of the (properly standardized) sample weighted sum and are shown to be much more accurate than those based on the negative association property.
On testing for informative selection in survey sampling
F. Jay Breidt, Colorado State University
Consider sampling from a finite population that is modeled as a realization from a stochastic generating mechanism, or superpopulation. The goal is to make inference about a distributional property of the superpopulation based on data from the sample. Informative selection occurs if the conditional distribution of a response in the sample, given that it was selected for observation, is not the same as the distribution of a response in the finite population. Inference must be modified to account for this informative selection. Methods of testing for informative selection, both parametric and nonparametric, are reviewed and extensions are discussed. Methods are compared analytically and via simulation.
How to generate uniform samples on large-scale data streams
Yann Busnel, IMT-Atlantique, Rennes
Within a network or distributed computer system, an ideal random sampling service should return a pointer to a node (which may be a computer, a process, a service, etc.), corresponding to an independent sample without bias to the group under consideration. This so-called uniform sampling service offers a simple primitive as a base brick for many applications in very large scale systems, such as information dissemination, metrology (via counting operations and statistical metrics), logic clock synchronization, etc. Unfortunately, the inevitable presence of malicious agents in these open systems hinders the construction of these sampling services.
Here we propose a solution to the problem of uniform sampling in large-scale computer systems in the presence of Byzantine behaviour. The latter reflect the non-compliance of the results of a system that does not meet its specifications. The Byzantine faults that are the most difficult to apprehend, come mainly from deliberate attacks aimed at making the system fail (sabotage, viruses, denial of service, etc.). We propose a first algorithm allowing to uniform on the fly a data (or items) stream of unbounded size, under the assumption that the exact probabilities of occurrence of the items are known. We model the behaviour of our algorithm using a Markov model and provide the results of the stationary and transient regime study. Our second algorithm releases the strong hypothesis of knowledge of item's probability of occurrence in the initial stream. These probabilities are then estimated on the fly using an aggregate data structure with a memory space proportional to the log of the size of the stream. We then evaluate the resilience of this algorithm to targeted and flooding attacks. In addition, we quantify the effort that the opponent must provide (i.e., the number of items to inject into the initial stream) to violate the uniformity property.
Properties of pivotal sampling : applications to spatial sampling and to sampling in dataflows
Guillaume Chauvet, ENSAI, Rennes
A large number of sampling algorithms with unequal probabilities have been proposed in the literature, see for example Tillé (2011) for a review. The choice of a sampling algorithm is based on both statistical and practical considerations. On one hand, statistical properties are required, such as the weak consistency and the asymptotic normality of estimators. On the other hand, it may be necessary to introduce constraints in the selection of units. For example, when sampling in a dataflow, it is attractive to have a sequential sampling procedure under which the decision of selecting or not a unit is done as soon as it enters the dataflow.
In this work, we consider the use of the pivotal method (Deville and Tillé, 1998), also known as Srinivasan sampling design (Srinivasan, 2001), which has a number of interesting properties. It is based on a principle of duels between units, and leads to a variance reduction if the order of the units in the population is informative. This is a sequential method, so that it can be particularly helpful when sampling in a dataflow. Also, it enables to avoid selecting neighbouring units which makes it useful in the context of spatial sampling, when we wish to select spatially balanced samples.
In this talk, we will describe the principles of the method, and prove that it guarantees good statistical properties for a Horvitz-Thompson estimator (weak consistency, central limit-theorem, exponential inequality) under mild assumptions. We will present two applications of the method. The first one is a modification of the Generalized Random Tesselation Sampling method, which is commonly used for spatial sampling. This is joint work with Ronan Le Gleut. The second work is related to sampling in a dataflow, with estimation on a sliding window. This is joint work with Emmanuelle Anceaume, Yann Busnel and Nicolo Rivetti.
A challenge for statisticians: the design-based spatial interpolation
Lorenzo Fattorini, Università degli Studi di Siena
Accurate and updated wall-to wall maps depicting the spatial pattern of ecological and economic attributes throughout the study area represents a crucial information for evaluations, decision making and planning. Traditionally maps, as well as most of the issues of spatial statistics, are approached in a model-based framework (e.g. Cressie 1993). Recently we have attempted to construct maps in a complete design-based framework simply exploiting the inverse distance weighting interpolator and deriving the properties from the characteristics of the sampling scheme adopted. We first approached the problem of making maps for finite population of spatial units, when the survey variable is the amount of an attribute within units (Fattorini et al. 2018a). Subsequently, we considered the problem of making maps for continuous populations when the survey variable is, at least in principle, defined at each point of the continuum representing the study area (Fattorini et al. 2018b). Finally, we have faced the problem of constructing maps for finite populations of marked points.
Our design-based approach to spatial mapping avoids the massive modelling involved in model-based approaches, i.e. the use of spatial models on lattices required for finite populations of spatial units (e.g. Cressie, Chapter 6), the use of second-order stationary spatial processes required for continuous populations (e.g. Cressie, Chapter 3) and the marked point processes in the plane required for finite populations of marked points (e.g. Cressie, Chapter 8). Design-based asymptotic unbiasedness and consistency of the resulting maps are achieved exploiting different asymptotic scenarios for the three cases, at the cost of supposing i) some forms of smoothness of the survey variables throughout the study area; ii) some sort of regularities that are necessary in the case of finite populations such as regularities in the shape of spatial units or regularities in the enlargements of the point populations; iii) asymptotically balanced spatial sampling schemes; iv) the use of distance functions sharing some mathematical properties. It is worth noting that iii) is satisfied by the more common sampling schemes adopted in spatial surveys and iv) does not constitute an assumption because it can be readily ensured by the user.
Cressie, N. (1993) Statistics for Spatial Data. New York: Wiley.
Fattorini, L., Marcheselli M, Pratelli L (2018a) Design-based maps for finite populations of spatial units. Journal of the American Statistical Association, to appear.
Fattorini, L., Marcheselli, M., Pisani, C., Pratelli, L. (2018b) Design-based maps for continuous spatial populations. Biometrika, to appear.
Survey methods and their use in Monte Carlo algorithms
Mathieu Gerber, University of Bristol
The problem of sampling in finite population arises in various Monte Carlo procedures and is notably at the heart of sequential Monte Carlo (SMC) algorithms. In this talk I will first explain the importance for this class of algorithms of what is called `resampling' schemes in the Monte Carlo literature, that can be viewed as a certain type of unequal probability sampling methods. I will then outline the desirable properties that resampling algorithms should have in the context of SMC before presenting some recent results on that topic as well as some open questions. In the second part of the talk I will discuss some other uses of unequal probability sampling algorithms within Monte Carlo methods, with applications ranging from the statistical analysis of Big data sets to the construction of low discrepancy point sets.
Estimation in the presence of influential units in finite population sampling: an overview
David Haziza, Université de Montréal
Influential units are those which make classical estimators very unstable. The problem of influential units is particularly important in business surveys, which collect economic variables, whose distribution are highly skewed (heavy right tail). There are two main inferential frameworks in survey sampling: the design-based framework and the model-based framework. To measure the influence of a unit under either framework, we use the concept of conditional bias of a unit and argue that it is an appropriate measure of influence measure. Using the conditional bias of a unit, we will show how to construct robust estimators/predictors of population totals. The robust estimators involves a psi-function, which depends on a tuning constant. The choice of the tuning constant will be discussed. Finally, the problem of internal and external consistency in the context of robust estimators will be presented.
Determinantal sampling design
Vincent Loonis, INSEE, Paris
In this presentation, recent results about point processes are used in sampling theory. Precisely, we define and study a new class of sampling designs: determinantal sampling designs. The law of such designs is known, and there exists a simple selection algorithm. We compute exactly the variance of linear estimators constructed upon these designs by using the first and second order inclusion probabilities. Moreover, we obtain asymptotic and finite sample theorems. We construct explicitly fixed size determinantal sampling designs with given first order inclusion probabilities. We also address the search of optimal determinantal sampling designs.
Joint work with Xavier Mary, Université Paris X - Nanterre
Functional central limit theorems for single-stage sampling designs
Rik Lopuhäa, TU Delft
In survey sampling one samples n individuals from a fixed population of size N according to some sampling design, and for each individual in the sample one observes the value of a particular quantity. On the basis of the observed sample, one is interested in estimating population features of this quantity, such as the population total or the population average. Well known estimators for population features that take into account the inclusion probabilities corresponding to the specific sampling design are the Horvitz-Thompson estimator and Hájèk’s estimator. Distribution theory for these estimators is somewhat limited, partly due to the dependence that is inherent to several sampling designs and partly due to the more complex nature of particular population features. In this talk I will present a num- ber of functional central limit theorems for different types of empirical processes obtained from suitably centering the Horvitz-Thompson and Hájèk empirical distribution functions. Basically, these results are obtained merely under conditions on higher order inclusion prob- abilities corresponding to the sampling design at hand. This makes the results generally applicable and allows more complex sampling designs that go beyond the classical simple random sampling or Poisson sampling. As an application I will use the results in combination with the functional delta method to establish the limit distribution of estimators for certain economic indicators, such as the poverty rate and the Gini index.
This is joint work with Hélène Boistard and Anne Ruiz-Gazen.
Revisiting design-based inference
Jean Opsomer, Colorado State University & Westat
Design-based inference is being challenged due to declining response rates and rising costs, and the increasing availability of large non-probability samples. In the first part of this talk, I aim to present arguments for the continued relevance of this traditional survey paradigm, but also propose ways to make it more appropriate to today’s data collection environment. In the second part, I present some recent results on nonresponse adjusted estimators using constraints. The results will illustrate how traditional approaches continue to be competitive with more sophisticated ones.
Large sample theory for merged data from multiple sources
Takumi Saegusa, University of Maryland
We study infinite-dimensional M-estimation for merged data from multiple data sources in a super population framework. A setting we consider is characterized by (1) duplication of the same units in multiple samples, (2) unidentified duplication across samples, (3) dependence due to finite population sampling. Applications include data synthesis of clinical trials, epidemiological studies, disease registries and health surveys. Our estimator is adopted from a well-known technique from analysis of multiple-frame surveys in sampling theory. The main statistical issue is a theoretical gap between sampling theory and theory of infinite-dimensional M-estimation. Sampling theory handles dependence well but it is often the case that relatively simple estimators are treated in the finite-population framework where randomness from a probabilistic model is considered fixed. Theory of infinite-dimensional M-estimation, on the other hand, deals with complex statistical models but it relies on results from empirical process theory most of which assume i.i.d. data. To fill this gap, we extend empirical process theory to biased and dependent samples with duplication. Specifically we develop the uniform law of large numbers and uniform central limit theorem with applications to general theorems for consistency, rates of convergence and asymptotic normality in the context of data integration. Our results are illustrated with simulation studies and a real data example using the Cox proportional hazards model.
Fast procedures for selecting unequal probability samples from a stream
Yves Tillé, University of Neuchâtel
Probability sampling methods were developed in the framework of survey statistics. Recently sampling methods are the subject of a renewed interest for the reduction of the size of large data sets. A particular application is sampling from a data stream. The stream is supposed to be so important that it cannot be stored. When a new unit appears, the decision to conserve it or not must be taken directly without examining all the units that already appeared in the stream. We will examine the existing possible methods for sampling with unequal probabilities from a stream. Next, we propose a general result about subsampling from a balanced sample that enables us to propose several new solutions for sampling and subsampling from a stream. Several new applications of this general result will be presented.
You can easily book an accommodation in the region. The exhaustive list of possible accommodations (according to the tourist information) in the region of Neuchâtel is available on the following link:
https://booking.juratroislacs.ch/Neuchatel/ukv/search?lang=en
Note that some of them are quite far from the city of Neuchâtel.
If you stay for a minimum of one night in a hotel, Bed & Breakfast or (registered) holiday apartment in the canton of Neuchâtel, you will be given the "Neuchâtel Tourist Card " for free. You can thus benefit for free from, among others:
- the public transport system of the region Neuchâtel (train, funicular and bus),
- an entry to 25 museums in the canton.
The city of Neuchâtel is easily reachable by train from all the swiss international airports (Geneva, Zürich and Basel). There is one direct train per hour from the airports of Geneva and Zürich. See the precise timetables on https://www.sbb.ch/en. The same site can be used to find timetables of any public transportation in Switzerland (local buses included).
The city itself is quite small, you should be able to reach by foot any accomodation in the city center from the railway station in maximum 15 minutes. The bus stop of the railway station is behind the station (in the opposite direction of the Lake). In front of the railway station, on the right, there is a taxi station.
The University has two different sites and the faculty of Sciences is located on the hill of "Le Mail". The closest bus stop is "Portes-Rouges" and the bus 107 goes there from the city center, via the railway station (direction Hauterive or Marin). From the bus stop, cross the bridge over the railways and the Faculty of Sciences is just on your right (big grey building, see the album here).
Trail at the Areuse gorges
The planned social activity is a hike in the Areuse Gorges, which are close to Neuchâtel. We will go there by train, from the railway station of Neuchâtel. The train leaves Neuchâtel at 14:41 on platform 1 (Sector D). The travel is free for holders of the Neuchâtel tourist card (anyone staying at an hotel can freely request it).
The train will take us until the station "Champ-du-Moulin" where we will start walking towards Boudry. The path is easy, see the map linked below (we will start from point 3 on the map). Good shoes are recommended for the hike.
If the weather is not good enough (the hike is not recommended if the trail is wet), we suggest to visit the Latenium, which is an archeological museum dedicated to the "La Tène Culture", a pre-celtic civilization (see Wikipedia page below).
Social dinner at Le Silex
The social dinner will take place at the restaurant Le Silex, on Tuesday at 19:15 (7:15 PM). From the city center, take the bus 101 towards Marin and leave the bus at the stop "Port" (Hauterive port). The restaurant is located at the port. From the railway station of Neuchâtel, take the funicular in the railway station (Fun'ambule) and then take the bus 101. The buses are included in the Neuchâtel Tourist Card.
Restaurant Le Silex with a map
http://lesilex.ch/bienvenue/contact/
General informations:
- https://www.neuchateltourisme.ch/en/leisure-activities/hiking/areuse-gorges.904.html
- https://en.wikipedia.org/wiki/La_T%C3%A8ne_culture
Map of the hike, with the profile :
Slides
Simon Barthelmé, Data sub-sampling with determinantal point processes (available here)
Yves Berger, An empirical likelihood approach for modelling survey data (paper on which the talk is based available here)
Patrice Bertail, Exponential bounds for survey sampling, towards applications to big-data (available here)
F. Jay Breidt, On testing for informative selection in survey sampling (available here)
Yann Busnel, How to generate uniform samples on large-scale data streams (available on request)
Guillaume Chauvet, Properties of pivotal sampling with applications to spatial sampling (available here)
Lorenzo Fattorini, A challenge for statisticians: the design-based spatial interpolation (available here)
Mathieu Gerber, Survey methods and their use in Monte Carlo algorithms (available here)
David Haziza, Estimation in the presence of influential units in finite population sampling: an overview (available on request)
Vincent Loonis, Determinantal sampling design (available here)
Rik Lopuhäa, Functional central limit theorems for single-stage sampling designs (available here)
Jean Opsomer, Revisiting design-based inference (available here)
Takumi Saegusa, Large sample theory for merged data from multiple sources (available here)
Yves Tillé, Fast procedures for selecting unequal probability samples from a stream (available here)


