Course List
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
L’analyse complexe est l’étude des fonctions d’une variable complexe, dérivables au sens complexe sur les ouverts de C, et appelées fonctions holomorphes. Ses premiers développements datent du XIXe siècle et sont dus principalement à trois mathématiciens : A. L. Cauchy (1798-1857), B. Riemann (1826-1866) et K. Weierstrass (1815-1897).
 |
 |
 |
| Cauchy | Riemann | Weierstrass |
À première vue, on pourrait penser qu’elle n’est qu’une répétition de l’étude des fonctions dérivables au sens réel, mais il n’en est rien !
En effet, la théorie de Cauchy – qui constitue la première partie traitée en détail – montre les liens surprenants qui existent entre les fonctions holomorphes, leur expression à l’aide d’intégrales de chemins (formule de Cauchy) et leur développement en séries de puissances. La théorie des fonctions d’une variable complexe est extrêmement élégante, et utile dans de nombreux domaines des mathématiques tels que la théorie analytique des nombre, l’analyse harmonique, la géométrie, pour ne citer que quelques exemples.
Un tel cours devrait être suivi par tout(e) étudiant(e) en mathématiques.
 |
 |
| La surface de Riemann correspondant à w 2 =z | La surface de Riemann correspondant à w 3 =z |
Mots clés
Fonctions holomorphes, intégrales de chemins, séries de puissances, formule de Cauchy, logarithme complexe, principe de prolongement analytique, singularités isolées, théorème des résidus, théorème de l’application ouverte, principe du maximum, mesures complexes et fonctions harmoniques, produits infinis, transformations conformes.
Références bibliographiques
- Real and complex analysis, W. Rudin, McGraw-Hill, 1966.
- Functions of One Complex Variable, J. Conway, Springer-Verlag, 1973.
- Théorie élémentaire des fonctions analytiques d’une ou plusieurs variables complexes – Deuxième cycle, H. Cartan, Hermann, 1997.
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
L’analyse fonctionnelle est la branche de l’analyse qui étudie les espaces de fonctions. Le mathématicien polonais Stefan Banach est souvent considéré comme le fondateur de l’analyse fonctionnelle moderne. Les espaces de base de l’analyse fonctionnelle sont les espaces vectoriels normés complets. De tels espaces sont appelés les espaces de Banach. Les espaces de Hilbert, constituent un cas particulier important, où la norme est issue d’un produit scalaire.
 |
 |
| Stefan Banach (1892 – 1945) | David Hilbert (1862 – 1943) |
Des objets d’étude importants en analyse fonctionnelle sont les opérateurs linéaires définis sur les espaces de Banach et de Hilbert. Ceux-ci mènent naturellement à la définition des C*-algèbres.
Pour tout nombre réel p ≥ 1, un exemple d’espace de Banach est donné par l’ensemble de toutes les fonctions mesurables au sens de Lebesgue dont la puissance p-ième de la valeur absolue a une intégrale finie.
Dans les espaces de Banach, une grande partie de l’étude implique l’espace dual : l’espace de toutes les formes linéaires continues. Cet espace dual permet d’introduire la notion de topologie faible, qui est importante dans la théorie des équations aux dérivées partielles.
Mots clés
Espaces vectoriels topologiques, opérateurs linéaires, théorie spectrale, opérateurs compacts, décomposition spectrale d’un opérateur borné, algèbres de Banach, introduction aux C*-algèbres, distributions, introduction aux espaces de Sobolev.
Références bibliographiques
- Analysis Now, G.K. Pedersen, Grad. Texts in Math., Springer-Verlag, 1989.
- Functional analysis, W. Rudin, McGraw-Hill 1981.
- A course in functional analysis, J.B. Conway, Springer, 1990.
- Introductory functional analysis with applications, E. Kreyzig, Wiley, 1978.
- Functional analysis, P. Lax, Wiley, 2002.
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
On peut dire que la géométrie métrique remonte à Euclide. Depuis deux siècles la géométrie différentielle (c’est-à-dire l’étude de la géométrie à l’aide du calcul différentiel) s’est beaucoup développée. On peut dire que la géométrie métrique consiste à faire de la géométrie sans calcul différentiel. Cela présente plusieurs avantages, notamment le fait de pouvoir aborder l’étude de nombreux exemples, et aussi quelques inconvénients. Depuis les années 80, et la parution du livre de Gromov-Lafontaine-Pansu en référence ci-dessous, la géométrie métrique s’est énormément développée, et cela dans des directions très diverses.
Le but de ce cours est d’en introduire les principes de bases afin qu’à la fin, un étudiant soit suffisamment armé pour se plonger dans chacun des ouvrages ci-dessous.
On trouvera sur la page Metric Spaces de Christina Sormani et la page Les Triangles d’Euclide, de Gauss et de Gromov (images des Maths) quelques mots sur la géométrie métrique.
Mots clés
Espaces métriques de longueur, géodésiques, théorème de Hopf-Rinow, notion de courbure en géométrie métrique, espaces d’Alexandrov, l’espace hyperbolique, la géométrie de Hilbert.
Références bibliographiques
- Lectures on Spaces of Nonpositive Curvature; W. Ballmann; DMV Seminar, Band 25, Birkhäuser, 1995.
- A course in metric geometry, D. Burago, Y. Burago, S. Ivanov; AMS, 2001.
- Metric spaces of nonpositive curvature, M. Bridson, A. Haefliger; Springer, 1999
- Structures métriques pour les variétés riemanniennes, M. Gromov, J. Lafontaine, P. Pansu; CEDIC, 1981
- Metric Spaces, Convexity and Nonpositive Curvature, A. Papadopoulos; European Mathematical Society, 2005.
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
La topologie algébrique consiste à décrire certain espaces topologiques, par exemple des surfaces, en leur associant des invariants de nature algébrique. Cela peut être un groupe (le groupe fondamental), un espace vectoriel ou une algèbre (cohomologie de De Rham). En général, la première partie du cours consiste à construire l’invariant algébrique associé à l’espace topologique. Dans un deuxième temps, on développe des méthodes algébriques pour calculer ces invariants dans des situations assez compliquées (théorème de Van Kampen, suite de Mayer-Vietoris). Enfin, on applique ce qui a été fait à la construction et à la compréhension d’exemples. Une question parmi d’autre est : comment montrer qu’une sphère ne peut pas se déformer en un tore ; ou encore, comment montrer qu’un tore à n anses ne peut pas se déformer en un tore à m anses si m est différent de n.
Selon les années, on abordera l’un ou l’autre de ces sujets. Sans que cela soit gravé dans le marbre, on traite en général alternativement ce qui tourne autour du groupe fondamental et des revêtements et ce qui tourne autour de la cohomologie de De Rham.
Mots clés pour un cours autour du groupe fondamental
Groupe fondamental, théorème de Van Kampen, groupes donnés par générateurs et relations, revêtements et leur classification.
Références bibliographiques
- Topologie algébrique, C. Godbillon, Hermann
- Algebraic topology, A. Hatcher, Cambridge University Press, 2002. Le cours traitera les chapitres 0 et 1 de ce livre qui peut être téléchargé
- Topology (second edition), J.R. Munkres, Prentice-Hall, 2000.
Mots clés pour un cours autour de la cohomologie de de Rham
Cas des 1-formes différentielles et degré des applications du cercle, algèbre extérieur, formes différentielle, cohomologie de De Rham, suite de Mayer-Vietoris, exemples, cohomologie à support compact, théorie du degré.
Références bibliographiques
- Differential Forms in Algebraic Topology, R. Bott, L. Tu, Springer, 1982.
- Differential Manifolds and Theoretical Physics, W. D. Curtis and F. R. Miller, Orlando, 1985.
- Differential Forms and Applications, M. P. Do Carmo, Springer, 1994.
- Eléments de topologie algébrique, C. Godbillon, Hermann, 1971.
- From Calculs to Cohomology, I. Madsen, J. Tornehave, Cambridge, 1997.
6 ECTS, 4h/semaine sur un semestre (2h cours + 2h TP)
Sur la terre :
- Il y a, à tout instant, deux points antipodaux qui ont exactement la même température et la même pression
- Le nombre de tous les sommets additionné de toutes les vallées est égal au nombre de tous les cols + 2.
Ces deux énoncés n’ont rien à voir avec la météorologie, la géographie ou la géologie mais avec la topologie de la sphère. Ce sont (de façon imagée) des théorèmes de «topologie différentielle».
La topologie différentielle est l’étude de la topologie des variétés (courbes, surfaces, etc.) et des fonctions différentiables définies sur ces variétés. Les questions posées sont de nature «globale» : Une variété peut elle se plonger dans une autre?, des variétés homéomorphes sont elles difféomorphes? A quelles conditions (sur la variété) une fonction admet elle un point fixe ?
Ce cours est une introduction à ces questions. Les concepts de bases (immersions, plongements, transversalité, théorèmes de Sard, etc.) sont introduits. Une partie du cours pourra être consacrée à l’étude des systèmes dynamiques sur les variétés (théorie de Morse) et à certaines applications des théorèmes de points fixes.
 |
 |
 |
| Surface de Boy | Ruban de Möbius (selon G. Escher) | Surface de Morin vue de dessus |
Mots clés
Variétés, Immersions, Plongements, Théorème de Sard, Degré de Brouwer, Introduction à la Théorie de Morse.
Références bibliographiques
- Differential Topology. Morris W. Hirsch, Springer-Verlag,
- Topology from the differentiable viewpoint. John W. Milnor, Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ. 1997 reprint of the 1965 original.
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
Le cours présente quelques problèmes classiques de théorie des nombres des 18ème et 19ème siècles (sommes de 2 carrés d’après Fermat et Euler, réciprocité quadratique de Gauss, somme de 4 carrés d’après Lagrange et Jacobi). Le point de vue choisi est “moderne”, et met l’accent sur les structures algébriques sous-jacentes (corps finis, entiers de Gauss, algèbres de quaternions, groupes de matrices).
Contenu:
- Théorie des nombres (sommes de 2 carrés, réciprocité quadratique, sommes de 4 carrés)
- Algèbre (quaternions, groupes de matrices 2-fois-2)
- Applications en théorie des graphes (construction des graphes “de Ramanujan” de Lubotzky-Phillips-Sarnak, 1986).
 |
 |
| Timbre indien en l’honneur de Ramanujan | Timbre irlandais commémorant la découverte des quaternions par Hamilton en 1843 |
Mots-clés
Sommes de 2 et 4 carrés, loi de réciprocité, quaternions, groupes finis de matrices, graphes.
Références bibliographiques
- H.E. Rose, A course in number theory, Oxford Science Publications, 1988
- Giulana DAVIDOFF, Peter SARNAK & Alain VALETTE, Elementary Number Theory, Group Theory and Ramanujan Graphs, Cambridge Univ. Press, 2003.
Liens
- Les graphes de Ramanujan (Wikipedia)
- La loi de réciprocité quadratique (PlanethMath.org)
- Théorème de Fermat sur les sommes de 2 carrés (Wikipedia)
- Théorème de Lagrange sur les sommes de 4 carrés (Wikipedia)
- Les quaternions (Wikipedia)
6 ECTS, 4h par semaine sur un semestre (2h cours + 2h TP)
La théorie géométrique des groupes est un domaine des mathématiques consacré à l’étude des groupes de type fini, en explorant les liens entre les propriétés algébriques de ces groupes et les propriétés géométriques des groupes sur lesquels ces groupes agissent (c-à-d., les espaces où les groupes en question sont réalisés comme groupes de symétrie). Une idée importante – due à Gromov – est de considérer les groupes de type fini eux-même comme des objets géométriques, en les voyant comme des espaces métriques, où la distance est donnée par la longueur des mots.
Contenu
- Chapitre 1: Groupes libres (définitions; lemme du ping-pong; paradoxe de Hausdorff-Banach-Tarski; moyennabilité; le groupe F de Thompson)
- Chapitre 2: Groupes et quasi-isométries (les groupes comme espaces métriques; quasi-isométries; actions propres; croissance des groupes; retour sur la moyennabilité)
 |
 |
 |
| Un pavage hyperbolique (graphe de Cayley d’un groupe d’isométries hyperboliques) | Un pavage hyperbolique ré-interprété par l’artiste hollandais M.C. Escher | Graphe de Cayley du groupe libre sur deux générateurs |
Liens
- La géométrie des groupes sur le site “Images des Mathématiques”
- Théorie de la géométrie des groupes (Wikipedia)
- Le site de Jon McCammond, qui fait référence dans le sujet
Mots-clés
groupes libres, groupes résolubles, propriétés virtuelles, alternative de Tits, moyennabilité, graphes de Cayley, croissance.
Références bibliographiques
- P. de la Harpe, Topics in geometric group theory. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 2000. ISBN 0-226-31719-6;
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
Depuis Euclide, la répartition des nombres premiers à l’intérieur des entiers n’a pas cessé de fasciner les mathématiciens – un des “problèmes du millénaire” (= les problèmes à un million de dollars), l’Hypothèse de Riemann sur les zéros de la fonction zeta, équivaut à une formule asymptotique fine pour le n-ème nombre premier. Le cours donnera quelques résultats, récents et moins récents, sur la répartition des premiers.
 |
Module de la fonction zeta, avec la droite critique (coloriée en bleu) en x=1/2, le pôle en x=1, un zéro non trivial dans le coin supérieur droit, son complexe conjugué dans le coin inférieur droit, et les zéros triviaux sur l’axe réel en x=-2,-4-6, etc… |
Contenu
- Chapitre 1: Les premiers résultats allant au delà d’Euclide (Euler et Tchebichev)
- Chapitre 2: Nombres premiers dans les progressions arithmétiques (d’après Dirichlet)
- Chapitre 3: Le théorème des nombres premiers de Hadamard et de la Vallée-Poussin.
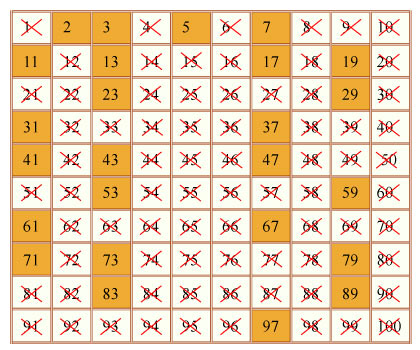 |
 |
| Le crible d’Eratosthène |
Mots-clés
nombres premiers, congruences, fonction zêta, fonctions L, prolongement analytique.
Références
- H.E. Rose, A course in number theory, Oxford Science Publications, 1988
- J.-P. Serre, Cours d’arithmétique, Presses Univ. France, 1977
- M. du Sautoy, The music of the primes, Harper Collins Publishers, 2003.
Liens
- Le site de Markus du Sautoy (fonctions zeta)
- Le site des grands nombres premiers
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
 |
 |
 |
La géométrie discrète et combinatoire est l’étude des objets et propriétés géométriques qui sont discrètes. De belles applications sont les formules calculant le volume d’un polyèdre, la densité maximale d’un empilement de boules, la géométrie des nombres avec ses applications en théorie de nombres, le théorème des quatre couleurs, etc.
Mots-clés
Enumération de points intégraux dans les polyhèdres (combinatoire), Sommes de Dedekind et séries de Fourier finies (théorie de nombres), Polygones et polytopes (géométrie), Fonctions génératrice, la formule de Pick, polynome d’Ehrhart, Carrés magiques.
Références bibliographiques
- Matthias Beck, Sinai Robins, Computing the continuous discretely. Undergraduate Texts in Mathematics. Springer, 2007.
- Peter Gruber, Convex and discrete geometry. Grundlehren der Mathematischen Wissenschaften, 336. Springer, 2007.
6 ECTS, 4h par semaine sur un semestre (2h cours + 2h TP)
Les chaînes de Markov permettent de décrire et d’analyser des systèmes qui évoluent dans le temps et présentent un caractère aléatoire. Objet central en théorie des probabilités, elles sont fréquemment utilisées dans des domaines aussi divers que la physique, la biologie, les sciences sociales ou l’informatique.
Ce cours est une introduction aux chaînes de Markov. L’accent est mis sur l’étude de l’asymptotique : critères de récurrence, théorèmes ergodiques, vitesse de convergence, etc. Au delà de ces résultats classiques, une partie du cours est consacrée à la présentation d’applications modernes : algorithmes de Metropolis, de Propp et Wilson, recuit simulé ; et à l’exposé des outils mathématiques réemment développés pour étudier ces applications.
Modélisation Markovienne. Chaînes de Markov sur un espace fini : théorèmes ergodiques, simulation, algorithmes de Métropolis, recuit simulé, vitesse de convergence, trou spectral, forme de Dirichlet, constante de log-sobolev. Chaînes de Markov sur un espace dénombrable : récurrence, transience, marches aléatoires, files d’attentes. Références bibliographiques
- Promenade aléatoire. Chaînes de Markov et simulations, martingales et stratégie, M. Benaïm, N. El Karoui , éditions de l’école polytechnique, 2004
- Lectures on finite Markov chains, L. Saloff-Coste, Saint Flour lectures notes, Springer, 1997.
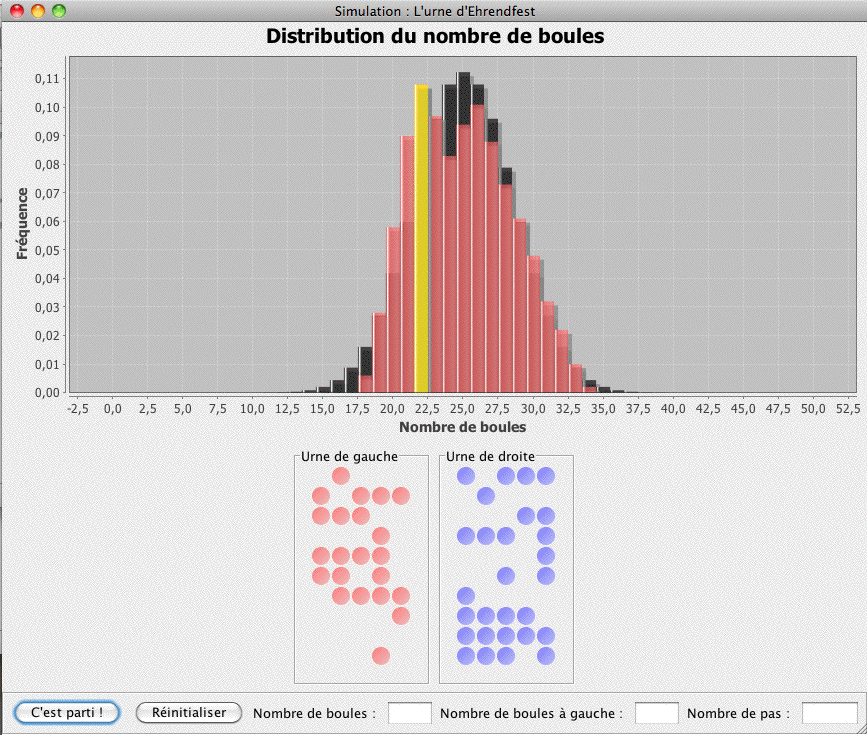
|
L’urne d’Ehrenfest
|
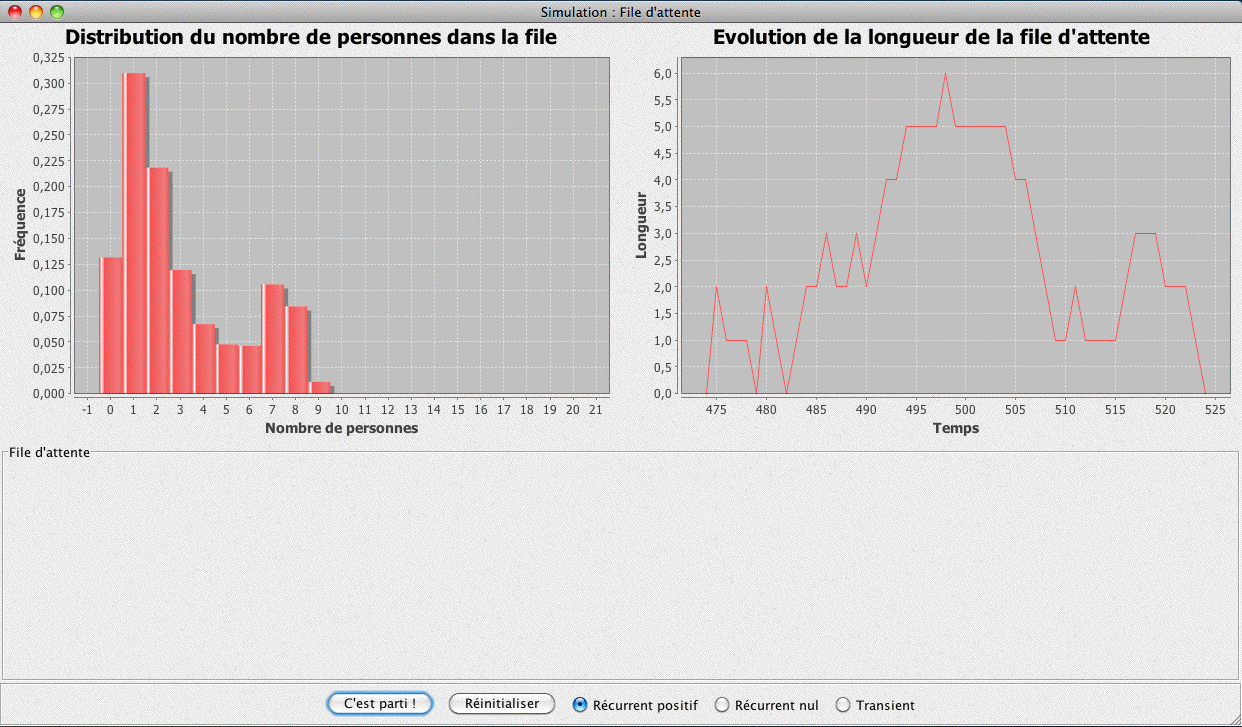
|
Une file d’attente
|
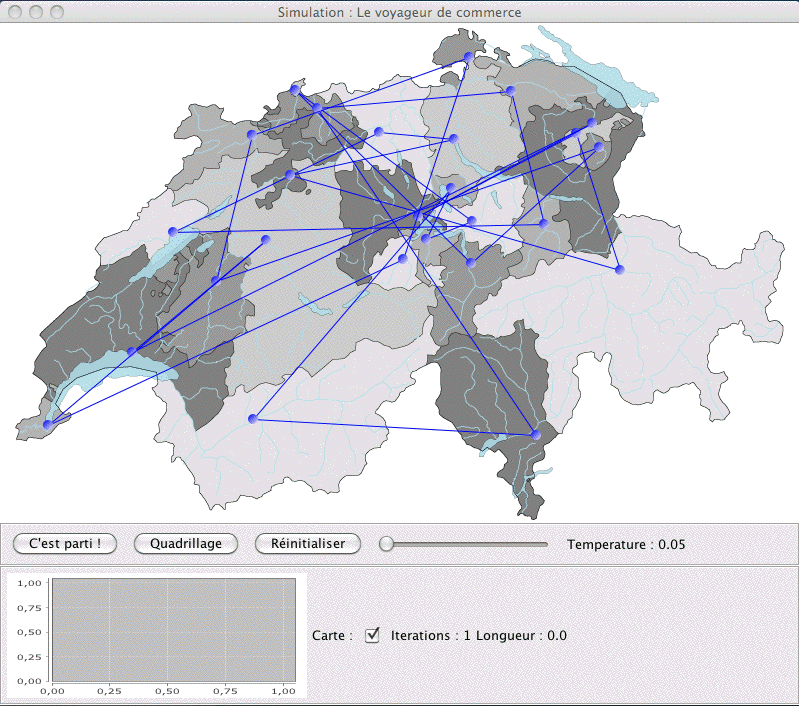
|
L’algorithme du recuit simulé appliqué au voyageur de commerce
|
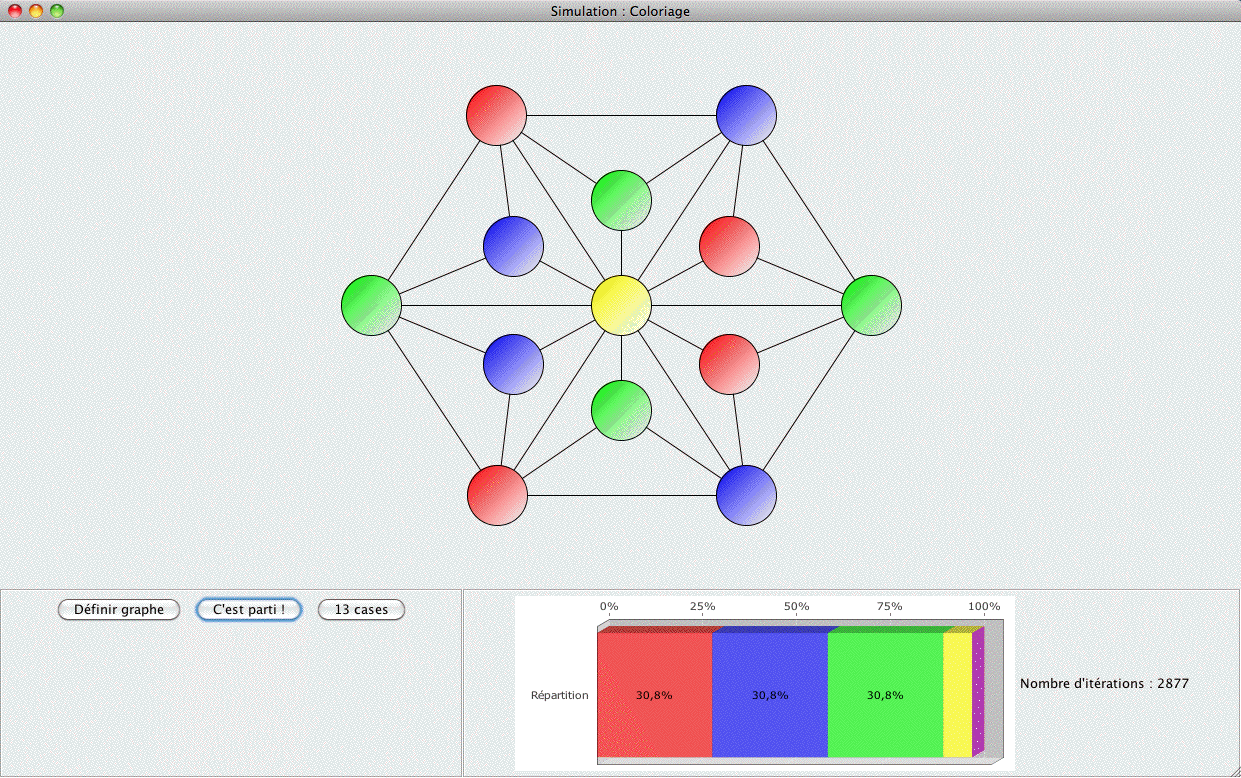
|
L’algorithme du recuit simulé appliqué au problème des quatre couleurs
|
6 ECTS, 4h/semaine sur un semestre (2h cours + 2h TP)
Née dans la première moitié du 20ème siècle, la théorie des martingales est un outil puissant pour étudier une large classe de systèmes dont l’évolution temporelle présente un caractère aléatoire (cours de la bourse, gains au casino, molécules de gaz en interactions, ….).
Ce cours est une introduction à la théorie des martingales à temps discret. Les résultats principaux (théorèmes de convergences, théorèmes d’arrêt, inégalités maximales) sont exposés ainsi que de nombreux exemples concrets d’applications : processus de branchement, jeux de hasard, modèles d’urnes appliquées à l’économie …
 |
|
| Marche aléatoire des photons du soleil |
Mots clés
Théorèmes de convergence, temps d’arrêt, inégalités maximales, problème d’arrêt optimal.
Références bibliographiques
- Promenade aléatoire. Chaînes de Markov et simulations, martingales et stratégie, M Benaïm, N El Karoui , éditions de l’école polytechnique, 2004
- Probability with martingales, D. Williams, 1997, Cambridge Mathematical Textbooks
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
Le calcul différentiel est un outil extrêmement puissant, et, dans un cours de géométrie différentielle, on l’applique à l’étude de la géométrie. Par exemple, comment décrire qu’une surface est courbée, comment calculer le chemin le plus court entre deux points ?
Dans ce cours, on introduit le concept de variété riemannienne, qui est une généralisation naturelle, mais plus abstraite, de la notion intuitivement bien connue de surface. Une partie importante du cours est consacrée à construire et à comprendre des exemples.
On trouvera ici une description de la géométrie riemannienne pour non spécialistes. La géométrie différentielle et la géométrie riemannienne sont le cadre naturel pour étudier les systèmes dynamiques, notamment le flot géodésique, les surfaces minimales. La géométrie riemannienne est également un des outils mathématiques de base pour la théorie de la relativité générale.
Mots clés
variété et sous-variétés différentielles, espaces tangents, dérivée de Lie, flot d’un champ de vecteurs, métrique riemannienne, groupe de Lie, connexion de Lévi-Civita, géodésiques, flot géodésique, courbure. Exemples : espaces projectifs réels et complexes, groupe de Heisenberg, quotient par un groupe discret d’isométrie, l’espace hyperbolique.
Références
- An Introduction to Differentiable Manifolds and Riemannian Geometry, W.M. Boothby, Ac. Press, 1975.
- Differential Manifolds ans Theoritical Physics, W.D. Curtis, F.R. Miller , Ac. Press, 1985.
- Riemannian Geometry, M. P. Do Carmo , Birkhaüser, 1992.
- Riemannian Geometry, S. Gallot, D. Hulin, J. Lafontaine,Springer (différentes éditions)
- Introduction aux variétés différentielles, J. Lafontaine, Presses universitaires Grenoble, 1996.
Liens
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
Née des besoins de la mécanique statistique au XIXe siècle, la théorie ergodique désigne l’étude au sens large des actions de groupes sur des espaces mesurés ou sur des espaces topologiques. Nous étudierons principalement les actions de Z sur un espace mesuré X, c’est-à-dire la donnée d’une transformation T de Xvers X, qui préserve une mesure finie, et de ses itérées.
Nous présenterons les premiers résultats importants de la théorie (théorème de récurrence de Poincaré, théorème de Birkhoff) avec quelques applications à la théorie des nombres, par exemple, ainsi que le théorème d’équidistribution de H. Weyl, qui permettront d’étudier des exemples nombreux et variés. Le cours comprendra également les compléments nécessaires à la théorie de la mesure (par exemple, le théorème de Radon-Nikodym) et, en fonction du temps disponible, une introduction à la notion d’entropie.
Mots clés : Espaces probabilisés standards (y compris produits infinis), théorème de Radon-Nikodym, transformations ergodiques, mélangeantes, théorème de récurrence de Poincaré, Théorème ergodique de Birkhoff, homéomorphimes sur les espaces métriques compacts (ergodicité unique), transformations topologiquement transitives, applications.
Mots clé
Espaces mesurés, transformations ergodiques, transformations mélangeantes, espaces produits, shift de Bernoulli, rotation irrationnelle, théorème de récurrence de Poincaré, théorème ergodique de Birkhoff, théorème des nombres normaux, théorème de Radon-Nikodym, ergodicité unique, théorème d’équidistribution de Weyl, entropie.
Références bibliographiques
- An Introduction to Ergodic Theory, P. Walters, Springer-Verlag, 1982
- Invitation to Ergodic Theory, C. E. Silva, American Mathematical Society, 2008
- Problèmes ergodiques de la mécanique classique, V. I. Arnold et A. Avez, Gauthier-Villars, Paris, 1968
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
 |
 |
 |
Connaitre le futur c’est, lorsque c’est possible, comprendre les systèmes dynamiques formulés via des lois de la physique,
de la chimie, de la biologie, de l’économie, etc.
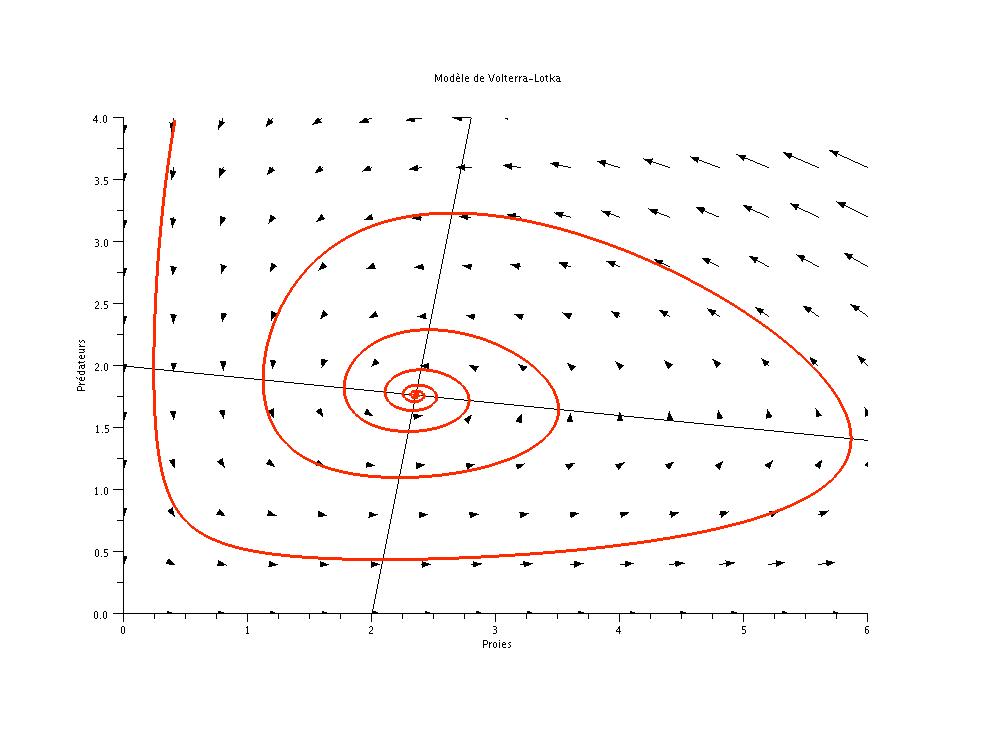
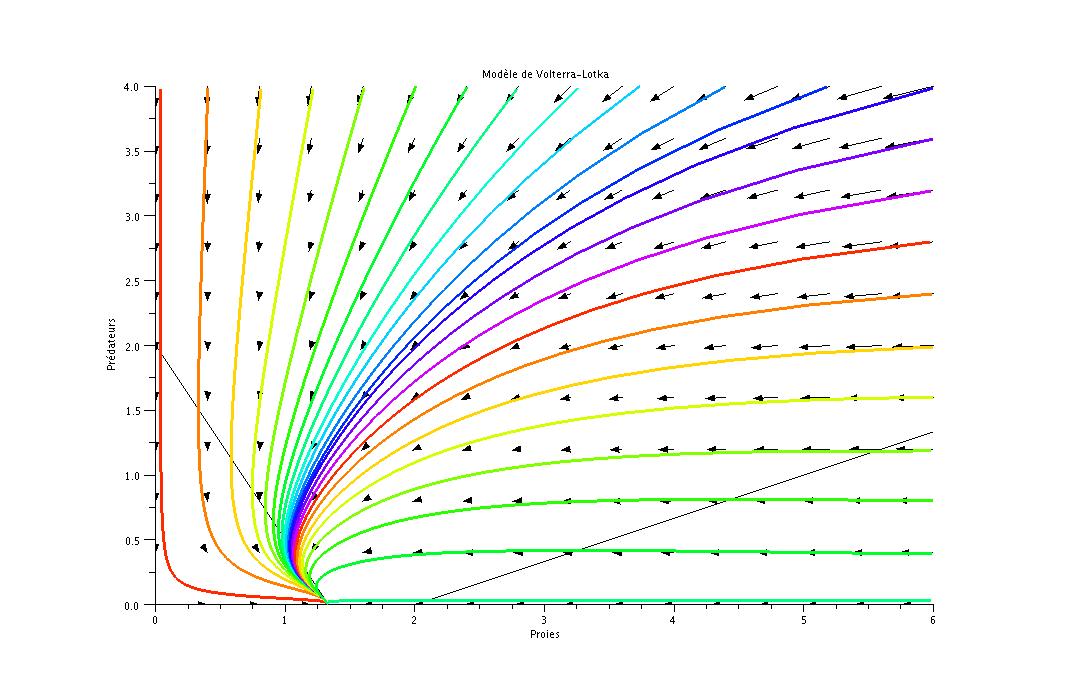
Dans ce cours, nous présentons quelques méthodes générales pour comprendre un systèmes dynamique. Ces méthodes sont alors appliquées aux problèmes de stabilité, aux systèmes proie-prédateurs et à la recherche d’orbites périodiques d’une boule sur une table de billard.
Mots clés
Etudes qualitatives des équations différentielles, portrait de phase, notions de récurrence, théorèmes de linéarisation, systèmes proies-prédateurs, théorie de Poincaré-Bendixson.
Références bibliographiques
- Differential equations, Dynamical Systems and An Introduction to Chaos, M.W. Hirsch, S. Smale, R. Devaney, Academic Press, 2004.
- An Introduction to Dynamical Systems : Continuous and Discrete, R.C. Robinson, Prentice Hall, 2004.
Lien
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
 |
 |
 |
Les systèmes Hamiltoniens sont les systèmes dynamiques “sans frottement”. Les petites oscillations ne décroissent pas, ce qui fait que de tels systèmes tendent à être compliqués. En particulier, les systèmes Hamiltoniens décrivent les systèmes de la mécanique classique, par exemple le mouvement des planètes, la propagation de la lumière, le mouvement d’un particule chargé soumis à un champ électromagnétique ou un potentiel.
Mots clés
Formalisme Hamiltonien, orbites fermées, flots géodésiques et magnétiques, théorème de Poincaré-Birkhoff, billard, problème des trois corps.
Références bibliographiques
- V. Arnold. Mathematical methods of classical mechanics. Graduate Texts in Mathematics, 60. Springer-Verlag,1998.
- Jürgen Moser, Eduard Zehnder, Notes on dynamical systems. Courant Lecture Notes in Mathematics, 12.; AMS
- Helmut Hofer, Eduard Zehnder, Symplectic invariants and Hamiltonian dynamics. Birkhäuser Verlag, Basel,1994.
- Serge Tabachnikov, Geometry and billiards. Student Mathematical Library, 30. AMS
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
Les équations aux dérivées partielles apparaissent de manière naturelle dans les sciences. Elles sont omniprésentes en mécanique des fluides, en l’électromagnétisme, en mathématiques financières, etc. Elles sont indispensables dans des domaines tels que les prévisions météorologiques, l’aéronautique, l’analyse d’images en radiologie.
Dans ce cours on étudie les propriétés des solutions de quelques équations aux dérivées partielles classiques intervenant pour la description de lois de conservation, de la diffusion de la chaleur ou de la propagation des ondes.
Remarquons qu’un des sept problèmes du prix du millénaire consiste à montrer l’existence d’une solution et la continuité par rapport aux données initiales d’un système d’équations aux dérivées partielles appelé équations de Navier-Stokes. Ces équations sont les fondements de la mécanique des fluides.
Mots clés
Références bibliographiques
- Partial differential equations, L. Evans, AMS, 1998.
- Partial differential equations, E. DiBenedetto, Birkhäuser, 1995.
- Partial differential equations, F. John, Springer, 198
6 ECTS, 4 h/semaine sur un semestre (2h cours + 2h TP)
La plupart des phénomènes physiques, chimiques, biologiques ou économiques peuvent être modélisés mathématiquement à l’aide d’équations aux dérivées partielles. Celles-ci, linéaires ou non, ne peuvent être explicitement résolues que dans des cas très simples. Grâce aux ordinateurs, on peut simuler et étudier des systèmes compliqués intervenant dans les sciences de l’ingénieur en résolvant ces équations de manière approchée. Ces simulations numériques permettent de réduire les coûts de développement et d’expérimentation en laboratoire de façon importante.
Dans le cadre de ce cours, nous allons étudier des méthodes numériques pour la résolution approchée d’équations aux dérivées
partielles. Nous nous limiterons à des problèmes relativement simples; mais les méthodes présentées se généralisent aisément. On s’intéressera en particulier problèmes hyperboliques, paraboliques et elliptiques.
Mots clés
Espaces de Sobolev, problèmes elliptiques, paraboliques et hyperboliques, méthode des différences finies, méthode des éléments finis, mise en œuvre informatique.
Références bibliographiques
Introduction à l’analyse numérique des équations aux dérivées partielles, P.A. Raviart, J.M. Thomas, Masson 1983.
The finite element method for elliptic problems, P.G. Ciarlet, North-Holland 1979.
Numerical solution of partial differential equations by the finite element method, C. Johnson, Studentlitteratur 1987.
Numerical methods for conservation laws, R.J. LeVeque, Birkhäuser, 1992.
Exemple de solutions numériques d’équations aux dérivées partielles
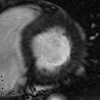 |
Simulation numérique du mouvement du coeur (coupe) |
6 ECTS, 4h/semaine sur un semestre (2h cours + 2h TP)
La théorie algébrique des graphes est un mélange d’algèbre linéaire et de combinatoire. Le but du cours est de présenter les méthodes du sujet, ainsi que quelques applications à l’informatique théorique.
Contenu: 1. Graphes; 2. Matrice d’adjacence et spectre; 3. L’algorithme PageRank; 4. Graphes réguliers et circulants; 5. Tour de taille et nombre chromatique; 6. Graphes expanseurs; 7. Cycles et coupures; 8. Lois de Kirchhoff
Mots-clés: graphe, matrice d’adjacence, spectre, graphes réguliers, graphes circulants, tour de taille, nombre chromatique, graphes expanseurs, cycles, coupure.
Références bibliographiques
- Norman L. BIGGS, Algebraic Graph Theory. Cambridge Tracts in Mathematics No. 67, Cambridge University Press, 1974;
- Giulana DAVIDOFF, Peter SARNAK & Alain VALETTE, Elementary Number Theory, Group Theory and Ramanujan Graphs, Cambridge Univ. Press, 2003.
 |
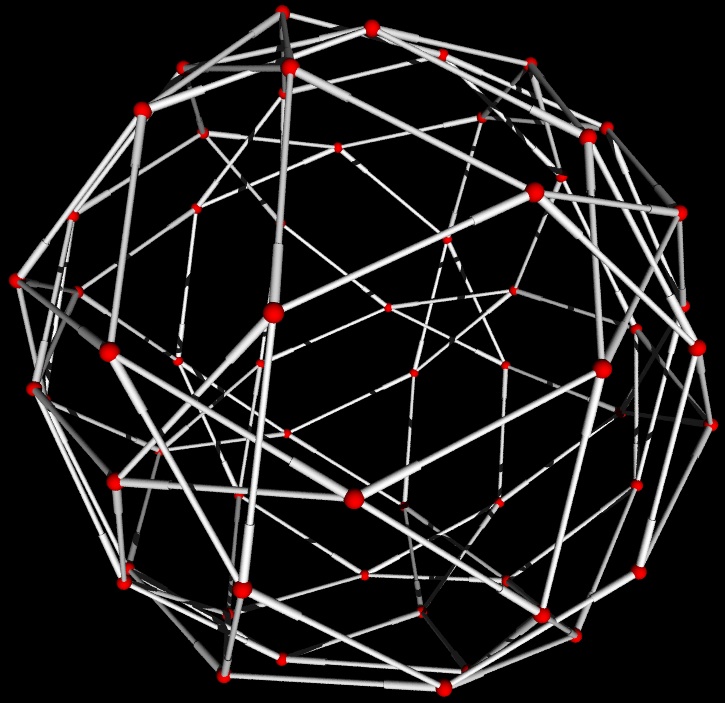 |
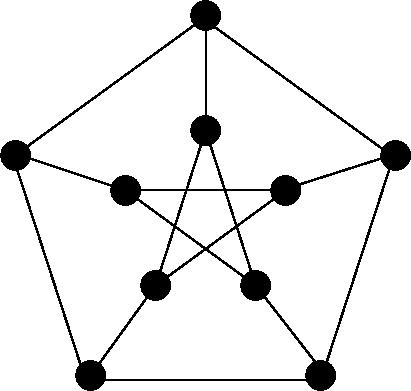
| Le graphe de Petersen | Le graphe de Cayley du groupe Alt(5) |
Liens
6 ECTS, 4h/semaine sur un semestre (2h cours + 2h TP)
L’écologie, terme inventé en 1865 par le biologiste et philosophe allemand Ernst Haeckelse se définit comme l’étude de l’interaction des organismes vivants et de leur environnement. Plus précisément, elle a pour objet l’évolution (temporelle et spatiale) des distributions des espèces et des conditions environnementales abiotiques (facteurs climatiques, chimiques, topographiques, etc.) et biotiques (ressources alimentaires, relations de prédation, compétition, parasitisme, mutualisme) qui déterminent cette évolution.
La prise en compte de ces conditions conduit donc à des modèles d’évolution qui dépendent du temps, de manière déterministe (cycles saisonniers) ou aléatoire (fluctuations environnementales), de l’abondance et de la structure spatiale des populations en interaction.
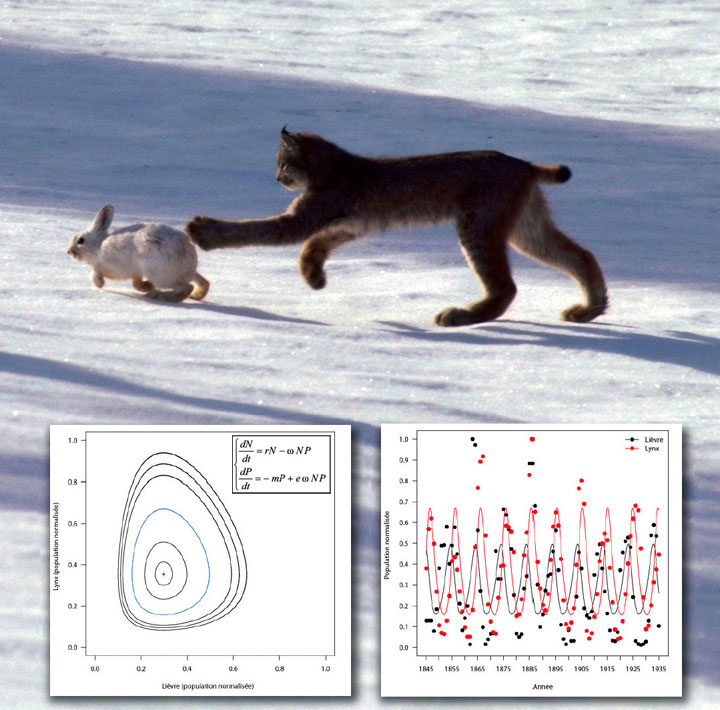
L’objet de ce cours est d’introduire les outils mathématiques utiles pour étudier ce type d’évolutions. Les notions et les résultats classiques des systèmes dynamiques déterministes (théorie des équations différentielles ordinaires) et aléatoires (théorie des chaines de Markov) sont exposés et chaque nouvelle notion est abondamment illustrée par des modèles et des exemples issue de l’écologie (dynamique des populations, génétique des populations).
Mots clés
Equations différentielles, flots, ensembles limites, modèles proies prédateurs, compétition, mutualisme, invasion et ondes progressives, chaînes de Markov, génétique des populations, méthodes de champ moyen.
Références bibliographiques
- Introduction aux systèmes dynamiques et aux chaînes de Markov, Applications à l’écologie. Notes de cours, M. Benaim
- Evolutionary Game and Population Dynamics, J. Hofbauer, K. Sigmund, Cambridge University Press, 1998
Liens:
- Un modèle de compétition entre des renards et des lapins